Уравнения состояния
УРАВНЕНИЯ СОСТОЯНИЯ,
ур-ния, выражающие связь между параметрами состояния физически однородной
системы при термодинамич. равновесии. Термическое У.с. связывает давление р
с объемом V и т-рой T, а для многокомпонентных систем - также
с составом (молярными долями компонентов). Калорическое У. с. вьюажает внутр.
энергию системы как ф-цию V, T и состава. Обычно под У. с., если специально
не оговаривается, подразумевают термич. У. с. Из него можно непосредственно
получить коэф. термич. расширения, коэф. изотермич. сжатия, термич. коэф. давления
(упругости). У. с. является необходимым дополнением к термодинамич. законам.
Пользуясь У. с., можно раскрыть зависимость термодинамич. ф-ций от V и р,
проинтегрировать дифференц. термодинамич. соотношения, рассчитать летучести
(фугитивносги) компонентов системы, через к-рые обычно записывают условия фазового
равновесия. Термодинамика устанавливает связь между У. с. и любым из термодинамических
потенциалов системы, выраженным в виде ф-ции своих естественных переменных.
Напр., если известна энергия Гельмгольца 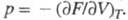 (свободная
энергия) F как ф-ция T и V, то У.
с. не может быть получено с помощью одних только законов термодинамики, оно
определяется из опыта или выводится методами статистич. физики. Последняя задача
очень сложная и м. б. решена лишь для упрощенных моделей системы, напр, для
идеального газа. У. с., применяемые для реальных систем, имеют эмпирич. или
полуэмпирич. характер. Ниже рассмотрены нек-рые наиб, известные и перспективные
У. с.
(свободная
энергия) F как ф-ция T и V, то У.
с. не может быть получено с помощью одних только законов термодинамики, оно
определяется из опыта или выводится методами статистич. физики. Последняя задача
очень сложная и м. б. решена лишь для упрощенных моделей системы, напр, для
идеального газа. У. с., применяемые для реальных систем, имеют эмпирич. или
полуэмпирич. характер. Ниже рассмотрены нек-рые наиб, известные и перспективные
У. с.
У. с. идеального газа имеет
вид pV=RT, где V-молярный объем, R - универсальная газовая
постоянная. Этому ур-нию подчиняются реальные газы при высоких разрежениях (см.
Клапейрона - Менделеева уравнение).
Св-ва реальных газов при
небольших и средних давлениях хорошо описываются вириальным уравнением: pV/RT
= 1 + B2 /V+B3 /V2 + ...,
где B2, В3 - второй, третий и т.д. вириальные коэффициенты.
Для данного в-ва они зависят лишь от т-ры. Вириальное У. с. обосновано теоретически;
показано, что коэф. B2 определяется взаимод. пар молекул,
В3 - взаимод. трех частиц и т.д. При больших плотностях в-ва
записанное выше разложение по степеням обратного объема расходится, поэтому
вириальное ур-ние непригодно для описания жидкостей. Оно служит лишь для расчета
летучестей компонентов газообразных B-B. Обычно ограничиваются членом B2
/V (редко B3/V2). В лит. приводят эксперим.
значения вириальных коэф., разработаны и теоре-тич. методы их определения. У.
с. со вторым вириальным коэф. B2 широко используют для моделирования
газовой фазы при расчетах фазовых равновесий в случае не слишком высоких давлений
(до 10 атм). Его применяют также для описания св-в разбавленных р-ров высокомол.
в-в (см. Растворы полимеров).
Для практич. расчетов фазовых
равновесий в широком диапазоне т-р и давлений важное значение имеют У. с., способные
описать одновременно св-ва жидкой и газовой фаз. В первые такое ур-ние было
предложено И. Ван-дер-Ваальсом в 1873:
р = RT(V-b)-a/V2,
где а и b - постоянные
Ван-дер-Ваальса, характерные для данного в-ва (см. Ван-дер-Ваальса уравнение).
Это У. с. имеет третий порядок относительно объёма V, любая изотерма при
параметрах состояния, меньших критич. значений (в докри-тич. области), имеет
три действит. положит, корня при фиксир. давлении. Наиб, из корней ур-ния соответствует
газовой фазе, наименьший - жидкой; средний корень ур-ния физ. смысла не имеет.
В сверхкритич. области параметров состояния изотермы имеют лишь один действит.
корень.
Кубич. зависимость давления
от объема сохраняется во MH. эмпирич. модификациях ур-ния Ван-дер-Ваальса. Чаще
других используют двухпараметрич. ур-ния Пенга - Робинсона (1976) и Редлиха
- Квонга - Соаве (1949, 1972). Эмпирич. постоянные этих У. с. можно определить
по критич. параметрам в-ва (см. Критическое состояние). Чтобы расширить
круг описываемых У. с. систем, набор рассматриваемых CB-B, диапазон т-р и давлений,
разработаны кубич. У. с., содержащие три и более эмпирич. постоянных. Важное
преимущество кубич. У. с.- их простота, благодаря чему при расчетах с помощью
ЭВМ не требуется слишком больших затрат машинного времени. Для мн. систем, образованных
неполярными или слабо полярными в-вами, эти У. с. обеспечивают требуемую для
практич. целей точность.
Если известны подробные
эксперим. данные о р-V-T-зависимостях, для их обобщения привлекают многопараметрич.
эмпирические У. с. Одно из наиб, распространенных У. с. такого типа - ур-ние
Бенедикта-Веббa Pубина (ур-ние БВР), разработанное в 1940 на основе вириального
У. с. В этом ур-нии давление р представлено в виде полинома плотности
в-ва с коэффициентами, зависящими от т-ры. Членами ряда высоких порядков пренебрегают,
а для компенсации включают в ур-ние экспоненциальный член. Это приводит к появлению
S-образных изотерм и дает возможность описывать жидкую фазу и равновесия жидкость
- газ.
Для неполярных и слабо
полярных в-в ур-ние БВР дает очень точные результаты. Для индивидуального в-ва
оно содержит восемь подгоночных параметров, для смеси дополнительно вводятся
параметры смешанного ("бинарного") взаимодействия. Оценка большого
числа подгоночных параметров - задача очень сложная, требующая многочисленных
и разнообразных эксперим. данных. Параметры ур-ния БВР известны лишь для неск.
десятков в-в, гл. обр. углеводородов и неорг. газов. Модификации ур-ния, направленные,
в частности, на повышение точности описания св-в конкретных в-в, содержат еще
большее число подгоночных параметров. Несмотря на это, добиться удовлетворит,
результатов для полярных в-в не всегда удается. Усложненность формы затрудняет
использование У. с. этого типа при расчетах процессов дистилляции, когда необходимо
выполнять многократную оценку летучестей компонентов, объема и энтальпии системы.
При описании смесей в-в
эмпирич. постоянные У. с. считаются зависящими от состава. Для кубич. У. с.
ван-дер-ва-альсового типа общеприняты квадратичные правила смешения, согласно
к-рым постоянные а и b для смеси определяют из соотношений:
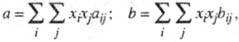
где xi,
xj - молярные доли компонентов, величины aij
и bij связывают с постоянными для индивидуальных в-в aii,
ajj и bii, bjj согласно комбинационным
правилам:
aij = (aiiajj)1/2(1-kij);
6ij = (bii+bjj)/2,
где kij
- подгоночные параметры смешанного взаимод., определяемые по эксперим. данным.
Однако квадратичные правила смешения не позволяют получить удовлетворит, результаты
для т. наз. асимметричных систем, компоненты к-рых сильно отличаются по полярности
и мол. размерам, напр, для смесей углеводородов с водой.
M. Гурон и Дж. Видал в
1979 сформулировали правила смешения нового типа, опирающиеся на модели локального
состава, к-рые успешно передают асимметрию концснтрац. зависимостей избыточного
потенциала Гиббса GE для жидких смесей и позволяют существенно
улучшить описание фазовых равновесий. Суть подхода состоит в том, что приравнивают
величины GE жидкого р-ра, получаемые из У. с. и рассчитываемые
согласно выбранной модели локального состава [ур-ния Вильсона, NRTL (Non-Random
Two Liquids equation), UNIQAC (UNIversal QUAsi-Chemical equation), UNIFAC (UNIque
Functional group Activity Coefficients model); CM. Растворы неэлектролитов].
Это направление интенсивно развивается.
Многие двухпараметрич.
У. с. (Ван-дер-Ваальса, вириаль-ное с третьим вириальным коэф. и др.) можно
представить в виде приведенного У. с.:
f(pпр,
Тпр, Vпр)= 0,
где pпр
= р/ркрит, Тпр=Т/Ткрит, Vпр=
V/Vкрит - приведенные параметры состояния. В-ва с одинаковыми значениями
рпр и Тпр имеют одинаковый приведенный объем
Vnp; совпадают также факторы сжимаемости Z = pV/RT, коэф.
летучести и нек-рые др. термодинамич. ф-ции (см. Соответственных состояний
закон). Более общий подход, к-рый позволяет расширить круг рассматриваемых
в-в, связан с введением в приведенное У. с. дополнит, параметров. Наиб, простые
среди них - фактор критич. сжимаемости Zкpит = ркритVкpит/RTкpит.
и ацентрич. фактор w= -Ig pпр -1 (при Тпр
= 0,7). Ацентрич. фактор является показателем несферичности поля межмол. сил
данного в-ва (для благородных газов он близок к нулю).
К. Питцер предложил пользоваться
для расчета фактора сжимаемости линейным разложением
Z(Tкpит,
ркрит) = Z0(Tкpит,
ркрит)+ wZ'(Tкpит,
ркрит),
где Z0 означает
фактор сжимаемости "простой" жидкости, напр, аргона, a Z' характеризует
отклонения от модели простой жидкости (см. Жидкость). Предложены корреляционные
соотношения, определяющие зависимости Z°(Tкpит, ркрит)
и Z'(Tкpит,
ркрит). Наиб, известны корреляции Ли и Кесслера, в к-рых
зависимость Z0 от Tкpит и ркрит
передается с помощью ур-ния БВР для аргона. Зависимость Z' от Tкpит
и ркрит установлена
при выборе в качестве "эталонной" жидкости н-октана. Принимается,
что Z'(Tкpит, ркрит) = [Z*(Tкpит,
ркрит)
- Z°(Tкpит, ркрит)]/w*,
где w* - фактор ацентричности н-октана, Z* - его фактор сжимаемости
согласно ур-нию БВР. Разработана методика применения ур-ния Ли-Кесслера и для
жидких смесей. Это У. с. наиб, точно описывает термодинамич. св-ва и фазовые
равновесия для неполярных в-в и смесей.
Наряду с вышеупомянутыми
эмпирич. У. с. важное значение приобрели ур-ния, обладающие возможностями учета
особенностей структуры молекул и межмол. взаимод. Они опираются на положения
статистич. теории и результаты численных экспериментов для модельных систем.
Согласно мол.-статистич. трактовке, ур-ние Ван-дер-Ваальса описывает флюид твердых
притягивающихся сфер, рассматриваемый в приближении среднею поля. В новых ур-ниях
уточняется прежде всего член ур-ния Ван-дер-Ваальса, обусловливаемый силами
межчастичного отталкивания. Значительно точнее приближение Кариахана- Старлинга,
опирающееся на результаты численного моделирования флюида твердых сфер в широком
диапазоне плотностей. Оно используется во многих У. с., однако большие возможности
имеют У. с. модельных систем твердых частиц, в к-рых учитывается асимметрия
мол. формы. Напр., в ур-нии BACK (Boublik-Alder-Chen-Kre-glewski) для оценки
вклада сил отталкивания служит У. с. флюида твердых частиц, имеющих форму гантелей.
Для учета вклада сил притяжения употребляют выражение, аппроксимирующее результаты,
полученные методом мол. динамики для флюида с межчастичными потенциалами типа
прямоугольной ямы (см. Молекулярная динамика). Ур-ние BACK и его аналоги
позволяют с достаточной точностью описывать смеси, не содержащие высококипящих
компонентов.
Особенность описания смесей
высококипящих орг. B-B -необходимость учета дополнительной вращательно-колебат.
степени свободы, связанной со смещениями сегментов молекул-цепочек (напр., алкенов
C8). Для этих систем наиб, распространение получило ур-ние PHCT (Perturbed
Hard Chain Theory), предложенное Дж. Прауснитцем и M. До-нахью в 1978. Индивидуальное
в-во характеризуется тремя эмпирич. параметрами в ур-нии PHCT. Комбинационные
правила для смеси содержат один параметр смешанного взаимодействия. Дальнейшее
усовершенствование ур-ния PHCT основано на замене потенциала прямоугольной ямы,
описывающей притяжение молекул, потенциалом Леннард-Джонса [ур-ние PSCT (Perturbed
Soft Chain Theory)] и на учете анизотропии межмол. сил [ур-ние PACT (Perturbed
Anisotropic Chain Theory)]. Последнее ур-ние хорошо описывает фазовые равновесия
в системах с полярными компонентами даже без использования подгоночных параметров
парного взаимодействия.
Предложен ряд У. с., в
к-рых в явном виде учитываются взаимод. молекул, приводящих, напр., к образованию
водородных связей (ассоциация молекул), путем нахождения равновесных концентраций
ассоциатов с помощью действующих масс закона.
В 80-х гг. появились т.
наз. групповые У. с. [UNIWAALS (UNIfac van-der-WAALS equation), ур-ние Скьолда-Йорген-сена,
MHV-2, дырочное ур-ние, разработанное H. А. Смирновой и А. И. Викторовым, и
др.]. Они позволяют прогнозировать св-ва широкого круга систем, зная модельные
параметры для сравнительно небольшого числа структурных фрагментов (групп),
из к-рых состоят молекулы компонентов.
Все возрастающий интерес
к У. с. обусловлен прежде всего практич. потребностями разработки мн. совр.
технологий, связанных с абсорбционным разделением в-в, эксплуатацией нефтяных
и газовых месторождений и т. п., поскольку в этих случаях требуется количеств,
описание и прогнозирование фазовых равновесий в широком диапазоне т-р и давлений.
Однако пока не существует достаточно универс. У. с. Все упомянутые У. с. оказываются
неточными при описании состояний вблизи критич. точки и не предназначены для
рассмотрения критических явлений. Для этих целей разрабатываются специальные
У. с., но и они пока плохо приспособлены для конкретных практич. приложений.
У. с. твердых тел определяют,
напр., зависимость модулей упругости от т-ры и давления. Теоретич. расчеты свободной
энергии и модулей упругости проводятся для сравнительно простых моделей твердого
тела.
У. с. для систем, находящихся
во внеш. поле, разрабатываются и исследуются в соответствующих разделах физики.
В физике высоких давлений и т-р на основе эксперим. данных и общих теоретич.
представлений разработаны модели У. с., охватывающих все агрегатные состояния,
включая плотную плазму.
Лит.: Рид Р., Прауснитц Дж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., Л., 1982; У эйлес С., Фаловые равновесия в химической технологии, пер. с англ., ч. 1, M., 1989; Викторов А. И. (и д р.), "Ж. прикл. химии", 1991, т. 64, № 5, с. 961-78. Г. Л. Куранов.

